Grenzwert einer gebrochenrationalen Funktion

Häufig wird der Grenzwert durch Probieren bestimmt.

Dennoch lässt er sich bei gebrochenrationalen Funktionen auch mithilfe des Zähler- und Nennergrades ermitteln.

i

Tipp

Wenn ihr euch nicht sicher seid, empfiehlt es sich immer (zusätzlich) eine Wertetabelle anzulegen.

Zählergrad < Nennergrad

!

Merke

Ist der Zählergrad kleiner als der Nennergrad, dann ist der Grenzwert (für $+\infty$ und $-\infty$) immer null.

$\lim\limits_{x\to\pm\infty} f(x)=0$

Beispiel

$f(x)=\frac{x+1}{x^2-x-2}$

Der Zählergrad ist 1 ($x^1$) und der Nennergrad 2 ($x^2$). Es gelten die Grenzwerte:

$\lim\limits_{x\to+\infty} f(x)=0$ und $\lim\limits_{x\to-\infty} f(x)=0$


Zählergrad = Nennergrad

!

Merke

Sind Zähler- und Nennergrad gleich, dann ist der Grenzwert (für $+\infty$ und $-\infty$) der Quotient aus den beiden Koeffizienten.

$\lim\limits_{x\to\pm\infty} \frac{{\color{red}{a_n}} x^n + \dots + a_1 x + a_ 0}{{\color{red}{b_m}} x^m + \dots + b_1 x + b_ 0}=\color{red}{\frac{a_n}{b_m}}$

Beispiel

$f(x)=\frac{\color{red}{3}x^4+2x^2+10}{\color{red}{2}x^4+2x^2+1}$

Der Zählergrad ist 4 ($x^4$) und der Nennergrad ebenfalls. Es gelten die Grenzwerte:

$\lim\limits_{x\to+\infty} f(x)=\frac32$ und $\lim\limits_{x\to-\infty} f(x)=\frac32$


Zählergrad > Nennergrad

Hier gibt es mehrere Möglichkeiten. Es ist unnötig kompliziert alle auswenidg zu lernen. Daher am besten hier mit der Wertetabelle arbeiten.

Wer geübt mit Grenzwerten ist, kann hier Polynomdivision anwenden und dann den Grenzwert leicht ablesen.

Beispiel

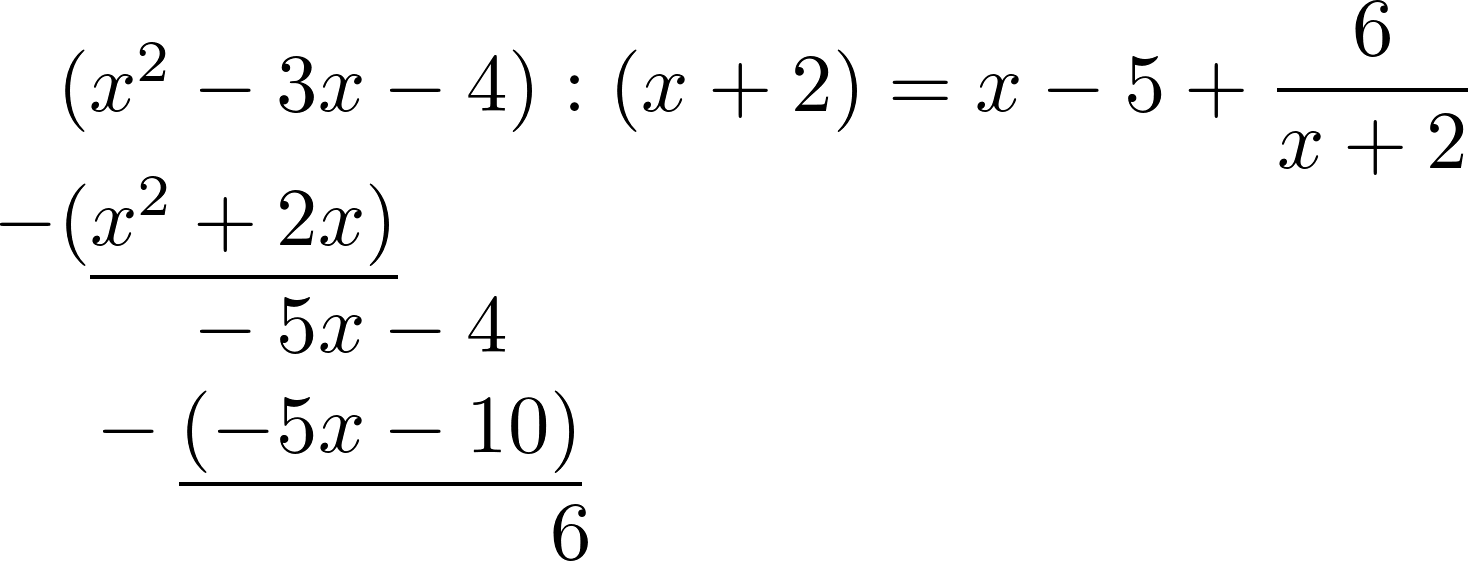
Wenn man für $x$ unendlich einsetzt bekommt man auch für den Grenzwert unendlich.

$\lim\limits_{x\to+\infty} \frac{x^2-3x-4}{x+2}$ $=\lim\limits_{x\to+\infty} (x-5+\frac{6}{x+2})$ $=„+\infty“$