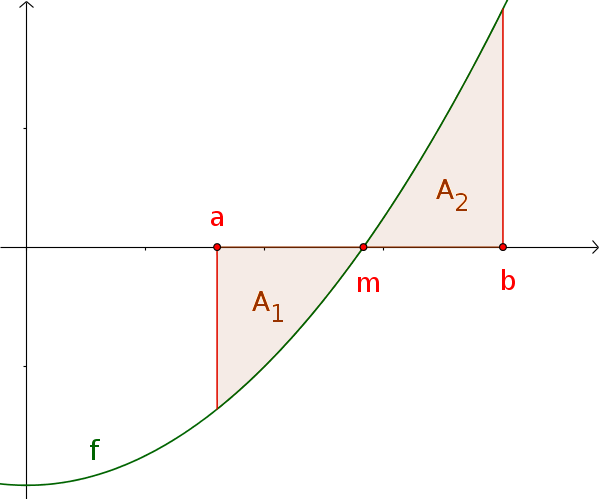
Der Flächeninhalt zwischen einem Graphen und der x-Achse lässt sich mit dem bestimmten Integral berechnen. Dabei solltest du folgendes beachten:
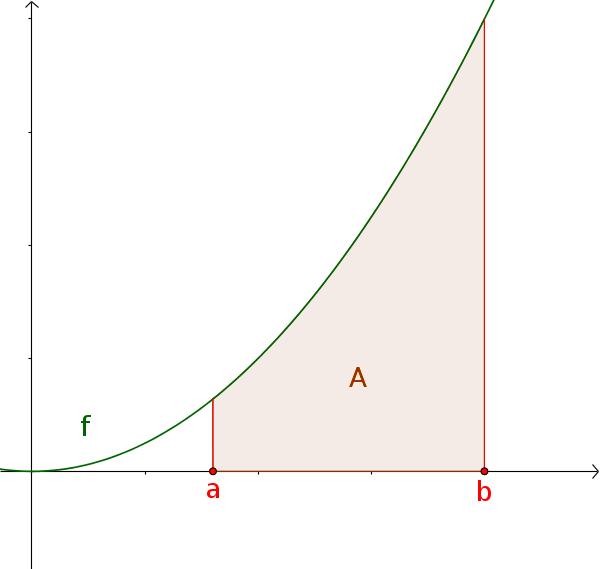
Der Flächeninhalt unter einer positiven Funktion $f(x)\ge0$ über $[a; b]$ entspricht dem bestimmten Integral.
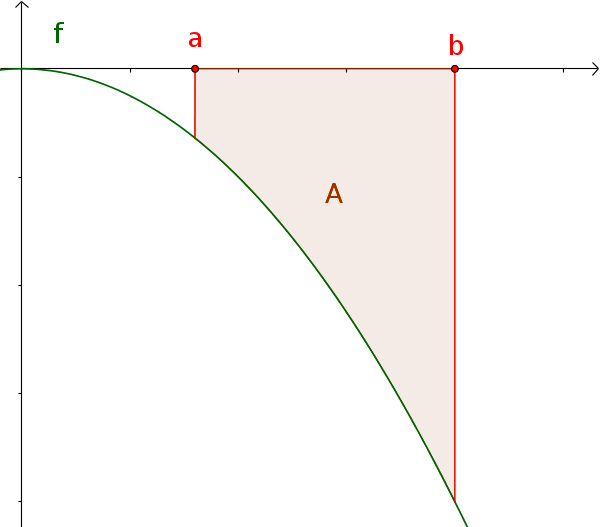
Der Flächeninhalt unter einer negativen Funktion $f(x)\le0$ über $[a; b]$ entspricht dem negativen bestimmten Integral.
Das bestimtme Integral einer Funktion $f$ mit Vorzeichenwechsel entspricht der Flächenbilanz über $[a; b]$.
Der Flächeninhalt ist also: