Steigungswinkel
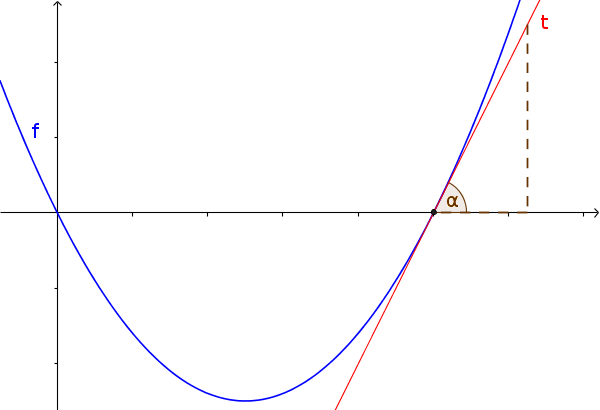
Mit der Ableitung kann man auch den Steigungswinkel an einer Stelle $x$ bestimmen.
!
Merke
Der Steigungswinkel $\alpha$ einer Funktion $f$ an der Stelle $x$ ist:
$\alpha=\arctan(f'(x))$
Beispiel
Berechne den Steigungswinkel der Funktion $f(x)=x^2$ an der Stelle $x=1$.
Stammfunktion: $f(x)=x^2$
Ableitung: $f'(x)=2x$
Einsetzen:
$\alpha=\arctan(f'(x))$
$\alpha=\arctan(f'(1))$
$f'(1)=2\cdot1=2$
$\alpha=\arctan(2)\approx63,43°$
i
Tipp
Häufig steht bei Taschenrechnern anstelle von $\arctan$ auch $\tan^{-1}$. Beides kommt dabei auf das Gleiche raus.
