Parallele Geraden haben überall einen konstanten Abstand.
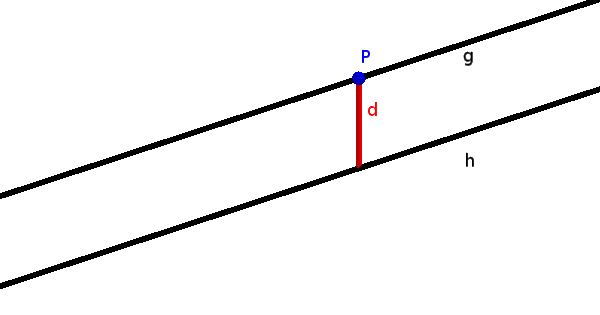
Auch hier können wir uns einfach einen Punkt auf der einen Gerade aussuchen und den Abstand eines Punktes zur Gerade berechnen.
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
$\text{h: } \vec{x} = \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}$
Da diese Methode nur bei parallelen Geraden funktioniert, muss man überprüfen, ob die Geraden parallel sind.
Dazu schauen wir, ob die Richtungsvektoren kollinear (parallel) sind.
$\vec{a}=r\cdot\vec{b}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=r\cdot\begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}$ $\Rightarrow r=3$
Es existiert ein $r$: Die Vektoren sind Vielfache voneinander und daher parallel.
Man kann jeden beliebigen Punkt der Gerade nehmen. Da man den Stützpunkt jedoch einfach ablesen kann, bietet sich dieser an.
$P(-1|0|3)$
Der Abstand kann nun wie unter Abstand Punkt und Gerade beschrieben berechnet werden.
Zuerst eine Hilfsebene mit $P$ als Stützpunkt und Richtungsvektor als Normalenvektor aufstellen.
$\text{H: } (\vec{x} - \vec{a}) \cdot \vec{n}=0$
$\text{H: } (\vec{x} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Der Lotfußpunkt ist der Schnittpunkt der Geraden $g$ und der Hilfsebene $H$. Zur Berechnung des Schnittpunkts wird die Geradengleichung für $\vec{x}$ in die Ebene eingesetzt.
$\left(\color{red}{\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}} - \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}\right)$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
$\begin{pmatrix} 2+r \\ 2+r \\ -2 \end{pmatrix}$ $\cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}=0$
Skalarprodukt berechnen
$(2+r)\cdot1+(2+r)\cdot1$ $+(-2)\cdot0=0$
$4+2r=0\quad|-4$
$2r=-4\quad|:2$
$r=-2$
$r$ in $g$ einsetzen, um Lotfußpunkt $F$ zu erhalten
$\vec{OF} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \color{red}{-2} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ $= \begin{pmatrix} 1-2 \\ 2-2 \\ 1-0 \end{pmatrix}$ $= \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$
$F(-1|0|1)$
Der Abstand des Lotfußpunktes zum Punkt $P$ ist auch der Abstand der Geraden zu diesem Punkt.
Der Abstand zwischen zwei Punkten lässt sich einfach mit Vektoren berechnen.
$d=|\vec{PF}|$ $=\left| \begin{pmatrix} -1-(-1) \\ 0-0 \\ 1-3 \end{pmatrix}\right|$ $=\left| \begin{pmatrix} 0 \\ 0 \\ -2 \end{pmatrix}\right|$ $=\sqrt{(-2)^2}$ $=2$
Der Abstand der beiden Geraden $g$ und $h$ beträgt 2 LE.