Im Gegensatz zu linearen Funktionen besitzen andere Funktionstypen keine konstante Steigung.
Zur Berechnung der durchschnittlichen Steigung zwischen zwei Punkten $P_1(x_0|f(x_0))$ und $P_2(x|f(x))$ nutzt man daher den Differenzenquotienten:
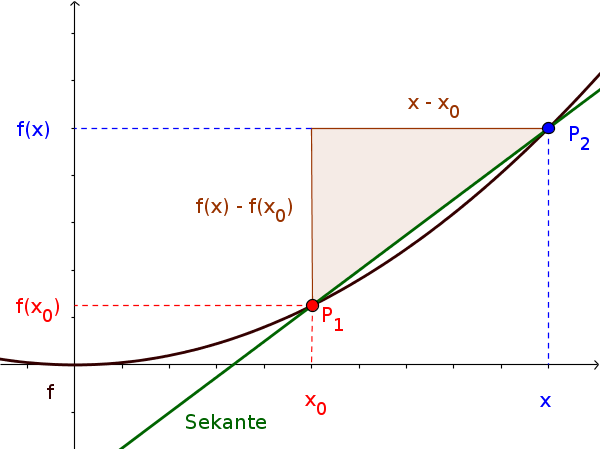
Der Differenzenquotient ist die Steigung der Sekanten, die durch die Punkte $P_1(x_0|f(x_0))$ und $P_2(x|f(x))$ geht.
Bestimme den Differenzenquotient der Funktion $f(x)=x^2$ von den beiden Punkten $P_1(2|f(2))$ und $P_2(5|f(5))$
$m=\frac{f(x)-f(x_0)}{x-x_0}=\frac{f(5)-f(2)}{5-2}$ $=\frac{5^2-2^2}{3}$ $=\frac{25-4}{3}$ $=\frac{21}{3}=7$